Matemática 3ero Bach 16-03-2020

Matemática 3ero de Bach  paralelos "A" "B" "BTU"

Días: Martes, Viernes

Planificación: https://recursos2.educacion.gob.ec/wp-content/uploads/2020/03/3ERO-BGU_Semana-1_Plan-de-contiguencia_2020-1.pdf

Fisica semana del 16 al 20 de marzo 2020

Fisica 2do de Bach paralelo "A" "B" "C"

Días: Miércoles, Viernes

Planificacion: https://recursos2.educacion.gob.ec/wp-content/uploads/2020/03/2DO-BGU_Semana-1_Plan-de-contiguencia_2020-1.pdf

Matemática semana del 16 al 20 de marzo 2020

Unidad Educativa tomas Oleas

Matemática 2do "C" Bach.
Semana del 16 al 20 de Marzo 2020

Planificación: https://recursos2.educacion.gob.ec/wp-content/uploads/2020/03/2DO-BGU_Semana-1_Plan-de-contiguencia_2020-1.pdf

DERIVADAS DE FUNCIONES REALES 4

FRASES DE MOTIVACIÓN PARA APRENDER MATEMÁTICA

1-No te preocupes por tus dificultades en matemáticas. Te puedo asegurar que las mías son aún mayores.-Albert Einstein.

2-Las matemáticas puras son, en su forma, la poesía de las ideas lógicas.-Albert Einstein.

3-La esencia de las matemáticas no es hacer las cosas simples complicadas, sino hacer las cosas complicadas simples.-S. Gudder.

4-Las matemáticas son un lugar donde puedes hacer cosas que no puedes hacer en el mundo real.-Marcus du Sautoy.

En este módulo se estudiara el límite de una función y sus aplicaciones, así también las derivadas de las funciones algebraicas, cálculo de máximos y mínimos, aplicación de las derivadas en diferentes problemas.

RELACIÓN GRÁFICA DE LAS FUNCIONES TRIGONOMÉTRICAS

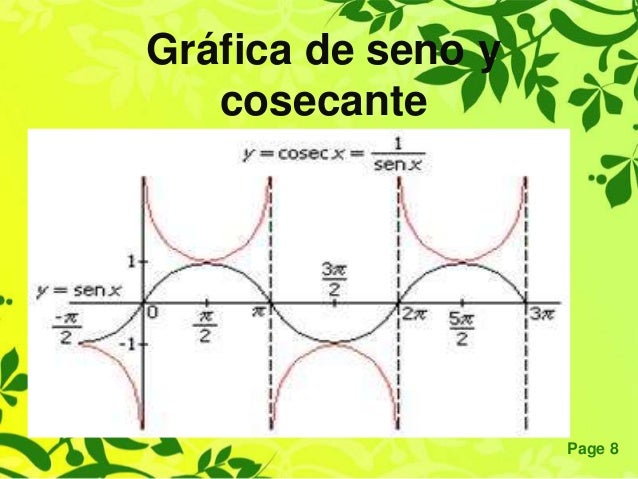
GRÁFICA DE LA RELACIÓN SENO-COSECANTE

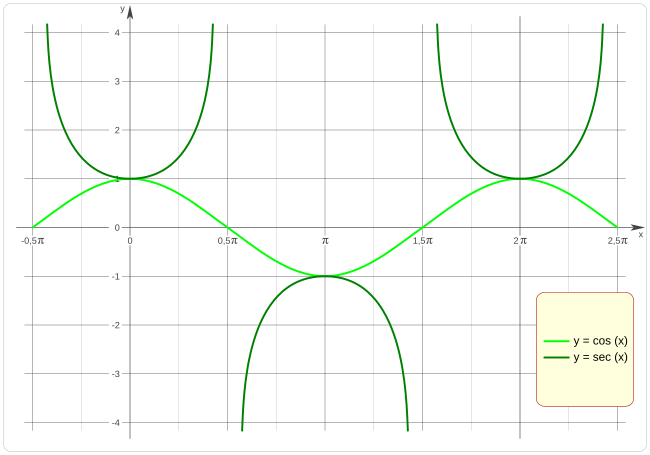
GRÁFICA DE LA RELACIÓN COSENO-SECANTE

GRÁFICA DE LA RELACIÓN TANGENTE-COTANGENTE

CARACTERÍSTICAS DE LA FUNCIÓN COTANGENTE-GRÁFICA

Las características fundamentales de la función cosecante son las siguientes:

1) Su dominio es    R - {k·π}   con   k∈Z .

2) Su recorrido es   R - (- 1, 1) .

3) No corta al eje X ni al eje Y.

4) Es impar, es decir, simétrica respecto al origen.

    cosec (- x) = - cosec (x)

5) Tiene infinitos máximos relativos en los puntos de la forma   (- π/2 + 2·k·π, - 1)  con   k∈Z .

    Tiene infinitos mínimos relativos en los puntos de la forma   (π/2 + 2·k·π, 1) con   k∈Z .

6) Es periódica de periodo   2π .

     cosec (x) = cosec (x + 2π)

7) Tiene asíntotas verticales en los puntos de la forma    x = k·π     con k∈Z .

8) No está acotada.

N.D. : No Definida

               

CARACTERÍSTICAS DE LA FUNCIÓN SECANTE-GRÁFICA

Las características fundamentales de la función secante son las siguientes:

1) Su dominio es    R - {π/2 + k·π}   con   k∈Z .

2) Su recorrido es   R - (- 1, 1) .

3) No corta al eje X.

    Corta al eje Y en el punto   (0, 1) .

4) Es par, es decir, simétrica respecto al eje Y.

    sec (- x) = sec (x)

5) Tiene infinitos máximos relativos en los puntos de la forma   (π + 2·k·π, - 1)  con   k∈Z .

    Tiene infinitos mínimos relativos en los puntos de la forma   (2·k·π, 1) con   k∈Z .

6) Es periódica de periodo   2π .

     sec (x) = sec (x + 2π)

7) Tiene asíntotas verticales en los puntos de la forma    x = π/2 + k·π     con k∈Z .

8) No está acotada.

N.D. : No Definida